计算机是用来存储和处理数据的。自然界中物体不可能是独立的,必定和别的物体之间有联系。比如人离不开衣服一样(除非在家裸睡,那也得睡在床上啊),总之物体不可能独立存在。同样的,在计算机的世界里,数据之间也是存在某些联系的,我们把这种联系称为数据结构。数据结构有逻辑结构和物理结构。逻辑结构有:链表,树,图等。物理结构表示的是数据在内存中的存储结构,可以是连续的,比如数组。也可以是不连续的内存,比如链表结构,可以用一个指针指向另一段内存的起始位置。在写 C 语言的时候,有很多数据类型,比如 int、 float、struct 等,为什么会有这么多数据类型呢?打个比方,现实世界中,有别墅,有胶囊公寓,这些都是用来住人的,家里人多的话住别墅,人少的话住胶囊公寓就行。房子就好比是计算机中的内存,有了数据结构后就能给数据分配合适的存储空间,这样不会浪费,效率会高点儿。
时间复杂度
我们怎么评估一个算法写的好坏呢?在不同平台上都运行一下代码,看看这个算法所需要的时间和占用内存的大小来评估算法的好坏,这显然是不科学的。于是就引入了时间复杂度和空间复杂度这两个概念。时间复杂度来评估算法的时间,空间复杂度来评估算法所需要占用的空间。在进行算法分析时,语句总的执行次数 T ( n ) 是关于问题规模 n 的函数,记作:T ( n ) = O ( fn ( n ) ) 。这样用 O ( ) 来体现算法时间复杂度的表示方式,我们称之为大 O 记法。推导大 O 阶方法要记住下面这三条规则:1. 用常数 1 来代表运行时间中所有加法常数。2. 只保留最高阶项。3. 如果最高阶存在且不为 1 ,则去除与这个项相乘的常数。下面来举列子依次说明怎么求大 O 阶。
例 1 常数阶
int a = 1; //执行一次
a = a + 1; //执行一次
printf("%d",a); //执行一次
上面的算法语句一共执行了 3 次,根据第一条规则:用常数 1 来代表运行时间中所有加法常数,那么它的时间复杂度为 O (1),我们把这种时间复杂度称之为常数阶。
例2 线性阶
int n = 100; //执行一次
for (int i = 0; i < n; i++) {
printf("%d",i); //执行 n 次
}
上面的 for 循环里的 printf 被执行了 n 次,一共执行了 n + 1 次,根据第二条规则:只保留最高阶项,那么它的时间复杂度为 O (n), 我们把这种时间复杂度称之为线性阶。
例3 平方阶
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; i++) {
printf("%d",i);
}
}
上面的 for 循环里的 printf 被执行了 n ^ 2 次,根据上面的规则,它的时间复杂度为 O ( n ^ 2) , 我们把这种时间复杂度称之为平方阶。
例4
while (i < n) {
i = i * 2;
}
上面的 while 里的语句被执行了 log2n 次,它的时间复杂度为 log2n。
总结:常用的时间复杂度所花费的时间从小到大依次是:
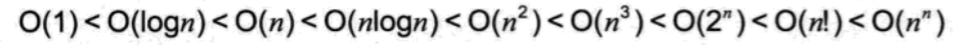
上面介绍了时间复杂度的推导方法。下面着重来学习下常用的排序方法,因为算法一直是编程的基础,而排序算法是学习算法的开始,排序也是数据处理的重要内容。排序的归类如下:
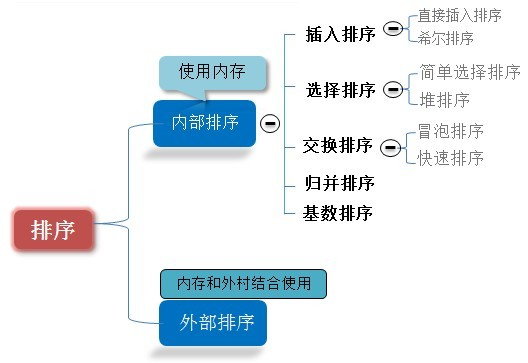
冒泡排序
基本思想:依次比较相邻的两个数,将小数放在前面,大数放在后面。
实现代码如下:
//冒泡排序
- (NSMutableArray *)bubbleSort:(NSMutableArray *)array {
NSInteger n = array.count;
for (NSInteger i = 0; i < n; i++) {
//这里注意下,一定是 n - 1 -i,要不会数组越界
for (NSInteger j = 0; j < n - 1 - i; j++) {
NSInteger a = [[array objectAtIndex:j] intValue];
NSInteger b = [[array objectAtIndex:j+1] intValue];
if (a > b) {
[array replaceObjectAtIndex:j withObject:[NSString stringWithFormat:@"%ld",b]];
[array replaceObjectAtIndex:j+1 withObject:[NSString stringWithFormat:@"%ld",a]];
}
}
}
return array;
}
复杂度为:n^2。
优化方法:
快速排序
基本思想是:
1.先从数列中取出一个数作为基准数(一般选择第一个)。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
实现代码如下:
//快速排序
-(NSMutableArray *)quickSortWithArray:(NSMutableArray *)array left:(NSInteger)left right:(NSInteger)right{
if (right > left) {
NSInteger x = [[array objectAtIndex:left] integerValue];
NSInteger i = left;
NSInteger j = right;
while (i < j) {
//从右向左找第一个小于x的数
while (i < j && [[array objectAtIndex:j] integerValue] >= x) {
j--;
}
if (i < j) {
[array replaceObjectAtIndex:i++ withObject:[array objectAtIndex:j]];
}
//从左向右找第一个大于等于x的数
while (i < j && [[array objectAtIndex:i] integerValue] < x) {
i++;
}
if (i < j) {
[array replaceObjectAtIndex:j-- withObject:[array objectAtIndex:i]];
}
}
[array replaceObjectAtIndex:i withObject:[NSString stringWithFormat:@"%ld",x]];
[self quickSortWithArray:array left:left right:i-1];
[self quickSortWithArray:array left:i+1 right:right];
}
return array;
}
直接插入排序
基本思想:直接插入排序,顾名思义,把一个数插入一个已经排好序的数据序列里。我们通常把第一数认为是已经排好序的一个数据序列。
实现代码如下:
//直接插入排序
- (NSMutableArray *)insertSort:(NSMutableArray *)array {
//假定第一个是排好序的,所以 i 从 1 开始
for (NSInteger i = 1; i < array.count; i++) {
NSInteger j = i;
NSInteger target = [[array objectAtIndex:i] integerValue];
while (j > 0 && target < [[array objectAtIndex:j - 1] integerValue]) {
[array replaceObjectAtIndex:j withObject:[array objectAtIndex:j - 1]];
j--;
}
[array replaceObjectAtIndex:j withObject:[NSString stringWithFormat:@"%ld",target]];
}
return array;
}
复杂度为:n^2。
希尔排序
基本思想:希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
实现代码如下:
//希尔排序
- (NSMutableArray *)shellSort:(NSMutableArray *)array {
NSInteger gap = array.count / 2;
while (1 <= gap) {
for (NSInteger i = gap; i < array.count; i++) {
NSInteger j;
NSInteger tmp = [[array objectAtIndex:i] integerValue];
for (j = i - gap; j >= 0 && tmp < [[array objectAtIndex:j] integerValue]; j -= gap) {
[array replaceObjectAtIndex:j + gap withObject:[array objectAtIndex:j]];
}
[array replaceObjectAtIndex:j + gap withObject:[NSString stringWithFormat:@"%ld",tmp]];
}
gap = gap / 2;
}
return array;
}
复杂度为:n^2。